“The Collatz Conjecture”

The Collatz conjecture, also known as the 3n + 1 conjecture, is a mathematical problem that involves a simple rule for generating a sequence of numbers. The conjecture is named after German mathematician Lothar Collatz, who introduced the problem in 1937. Despite its simplicity, the Collatz conjecture has remained unsolved for nearly a century and has captured the attention of mathematicians and computer scientists around the world.

The Collatz conjecture involves a rule for generating a sequence of numbers starting from any positive integer. The rule is as follows:

• If the current number is even, divide it by 2
• If the current number is odd, multiply it by 3 and add 1

For example, if we start with the number 5 and apply the rule, we get the following sequence:

5 -> 16 -> 8 -> 4 -> 2 -> 1

The conjecture is that, no matter which positive integer we start with, the sequence will always eventually reach the number 1. In other words, the conjecture states that every positive integer will eventually “collapse” to 1 through this process.

Despite its apparent simplicity, the Collatz conjecture has been remarkably difficult to prove or disprove. Despite numerous attempts, no one has been able to provide a rigorous mathematical proof that the conjecture is either true or false. The conjecture has been tested extensively using computers, and it has been found to hold for all integers up to 2⁶⁰, which is a very large number. However, a proof for all positive integers remains elusive.

The Collatz conjecture has attracted a great deal of attention from mathematicians and computer scientists over the years, and it has been the subject of numerous research papers and discussions. Despite its simplicity, the conjecture remains one of the most famous unsolved problems in mathematics, and it continues to challenge and intrigue researchers around the world.

In computer science,

the Collatz conjecture has been used as a test case for studying the behavior of algorithms and computational systems. For example, researchers have used the conjecture to study the performance of algorithms that generate and analyze sequences of numbers, and to test the limits of computational systems.

In mathematics, the Collatz conjecture has inspired research into a number of areas, including number theory and dynamical systems. Researchers have used the conjecture to study the properties of certain types of numbers and to explore the behavior of sequences of numbers under the Collatz rule.

The script below simulates the Collatz Conjecture in R

# Function to generate a Collatz sequence
collatz_sequence <- function(n) {
  # Initialize an empty vector to store the sequence
  seq <- c()
  
  # While n is not equal to 1, apply the Collatz rule
  while (n != 1) {
    # Add the current value of n to the sequence
    seq <- c(seq, n)
    
    # Apply the Collatz rule
    if (n %% 2 == 0) {
      # If n is even, divide by 2
      n <- n / 2
    } else {
      # If n is odd, multiply by 3 and add 1
      n <- 3 * n + 1
    }
  }
  
  # Add 1 to the sequence
  seq <- c(seq, 1)
  
  # Return the sequence
  return(seq)
}

# Test the function with a few different values of n
print(collatz_sequence(5))
print(collatz_sequence(7))
print(collatz_sequence(10))

This script defines a function called collatz_sequence that takes a positive integer n as input and generates a Collatz sequence using the 3n + 1 rule. The function initializes an empty vector to store the sequence and then enters a loop that applies the Collatz rule until n is equal to 1. The function then returns the final sequence. The script then tests the function with a few different values of n.

When run, this script should output the Collatz sequences for the numbers 5, 7, and 10. For example, the output for the number 5 should be 5 16 8 4 2 1.

# Install and load the ggplot2 library
install.packages("ggplot2")
library(ggplot2)

# Function to generate the length of a Collatz sequence
collatz_length <- function(n) {
  # Initialize a counter
  counter <- 0
  
  # While n is not equal to 1, apply the Collatz rule
  while (n != 1) {
    # Increment the counter
    counter <- counter + 1
    
    # Apply the Collatz rule
    if (n %% 2 == 0) {
      # If n is even, divide by 2
      n <- n / 2
    } else {
      # If n is odd, multiply by 3 and add 1
      n <- 3 * n + 1
    }
  }
  
  # Return the length of the sequence
  return(counter)
}

# Generate a vector of integers from 1 to 100
n <- 1:100

# Calculate the length of the Collatz sequence for each value of n
lengths <- sapply(n, collatz_length)

# Create a data frame with the values of n and lengths
df <- data.frame(n, lengths)

# Create a bar plot using ggplot
ggplot(df, aes(x = n, y = lengths)) +
  geom_col() + theme_bw() +
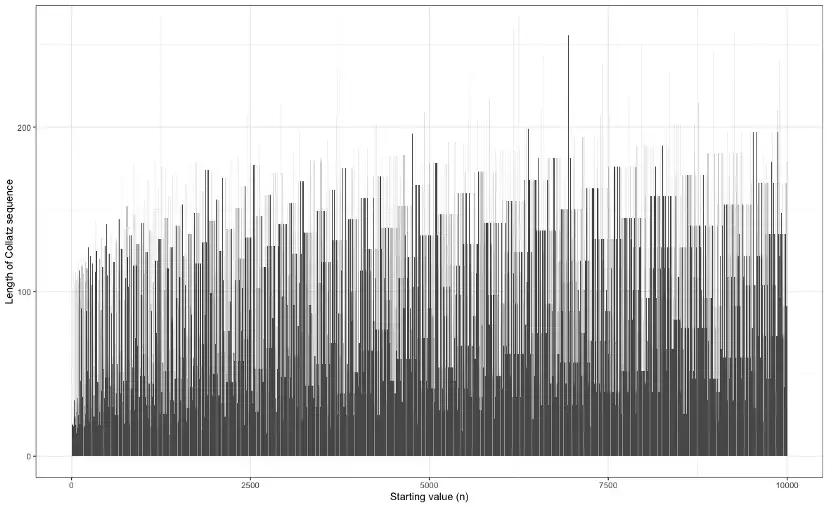
  labs(x = "Starting value (n)", y = "Length of Collatz sequence")

This script defines a function called collatz_length that takes a positive integer n as input and returns the length of the Collatz sequence for that value of n. The script then generates a vector of integers from 1 to 100 and calculates the length of the Collatz sequence for each value using the collatz_length function. The script then creates a data frame with the values of n and the lengths of the Collatz sequences and uses ggplot to create a bar plot that shows the length of the Collatz sequence for each value of n.

When run, this script should create a bar plot that shows the length of the Collatz sequence for each value of n from 1 to 100. The plot should show that the length of the Collatz sequence tends to increase as n gets larger.

Read More blogs in AnalyticaDSS Blogs here : BLOGS

Read More blogs in Medium : Medium Blogs