Welcome to the first part of our series, “Demystifying Data Science: A Comprehensive Guide for Beginners.” This series is designed to help aspiring data scientists gain a solid understanding of the fundamental concepts and techniques in the field of data science. We will explore various topics, including probability, statistics, machine learning, and data visualization, with a strong emphasis on practical examples and visual aids. In this first installment, we will delve into probability and statistics, covering essential concepts such as probability fundamentals, descriptive statistics, and inferential statistics. Stay tuned for more engaging and informative content in the upcoming parts of this series!

Introduction

Probability and statistics are essential disciplines for data scientists, analysts, and researchers. They provide a solid foundation for understanding, interpreting, and drawing meaningful conclusions from data. As the demand for data-driven insights and decision-making grows across various industries, a strong grasp of these concepts is crucial for anyone seeking a career in data science or looking to enhance their analytical skills.

In this blog post, we will introduce probability and statistics by exploring their basic concepts and terminology. We will explain the core principles and ideas that underpin these disciplines, using real-world examples and R code to help you visualize and understand these concepts in action. By incorporating visuals, we aim to make the material more engaging and easier to comprehend, allowing you to build a strong foundation for future learning.

Our journey will begin with probability fundamentals, including definitions, types of probability, and essential rules. We will then move on to descriptive statistics, discussing measures of central tendency, dispersion, and shape. Throughout the blog post, we will use the tidyverse package in R, focusing on ggplot2 for data visualization. This popular package offers a powerful and flexible way to create high-quality graphics, aiding in data exploration and communication.

By the end of this post, you will have a solid understanding of basic probability and descriptive statistics, supported by clear visualizations. This foundational knowledge will prepare you for more advanced topics and techniques in data analysis and machine learning, setting you on a path to success in the ever-evolving world of data science.

Stay tuned as we dive into the fascinating realm of probability and statistics, providing you with practical examples and insights to enhance your understanding and skills.

Probability Fundamentals

Probability is the study of randomness and uncertainty. It provides a way to quantify the likelihood of specific outcomes or events occurring in various situations. Understanding probability fundamentals is crucial for data science, as it underlies many statistical techniques and machine learning algorithms. In this section, we will elaborate on the basic concepts, principles, and rules of probability, using real-world data when possible.

I. Definitions:

• Experiment: An action or procedure that results in one of several possible outcomes. For example, rolling a die is an experiment with six possible outcomes (1, 2, 3, 4, 5, or 6).
• Outcome: The result of an experiment. In the die-rolling example, if the die lands on 3, then the outcome is 3.
• Event: A set of one or more outcomes. In the die-rolling example, an event could be the die showing an even number, which includes the outcomes {2, 4, 6}.
• Sample Space: The set of all possible outcomes of an experiment. For the die-rolling example, the sample space is {1, 2, 3, 4, 5, 6}.

II. Types of Probability:

• Classical: Based on the assumption that all outcomes are equally likely. In the die-rolling example, the classical probability of getting an even number is 1/2 (3 even numbers out of 6 possible outcomes).
• Relative Frequency: Based on the observed frequencies of outcomes in a sample. For instance, suppose we roll a die 100 times and observe 40 even numbers. The relative frequency of getting an even number is 40/100 = 0.4.
• Subjective: Based on an individual’s personal judgment or belief. A person may believe that it is more likely to rain tomorrow based on their interpretation of weather patterns and past experiences, even if objective data suggests otherwise.

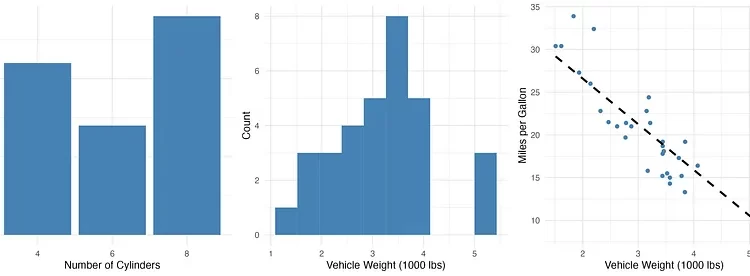
Let’s use a real-world dataset to illustrate the relative frequency approach. We will analyze the number of cylinders in vehicles from the mtcars dataset, which is included in R. We will calculate the relative frequency of vehicles with 4, 6, and 8 cylinders.

library(knitr)
data(mtcars)

cylinder_counts <- mtcars %>% count(cyl)
total_cars <- sum(cylinder_counts$n)
relative_frequencies <- cylinder_counts %>% 
mutate(relative_frequency = n / total_cars)

kable(relative_frequencies, caption = "Relative Frequencies of Cylinder Counts in Vehicles")

In the table above, the “cyl” column represents the number of cylinders in a vehicle, the “n” column shows the count of vehicles with the corresponding number of cylinders, and the “relative_frequency” column displays the relative frequency of each cylinder count in the dataset.

Now, let’s visualize the relative frequencies using ggplot2.

library(tidyverse)

ggplot(relative_frequencies, aes(x = factor(cyl), y = relative_frequency)) +
  geom_col(fill = "steelblue") +
  labs(title = "Relative Frequency of Cylinder Counts in Vehicles",
       x = "Number of Cylinders",
       y = "Relative Frequency") +
  theme_minimal()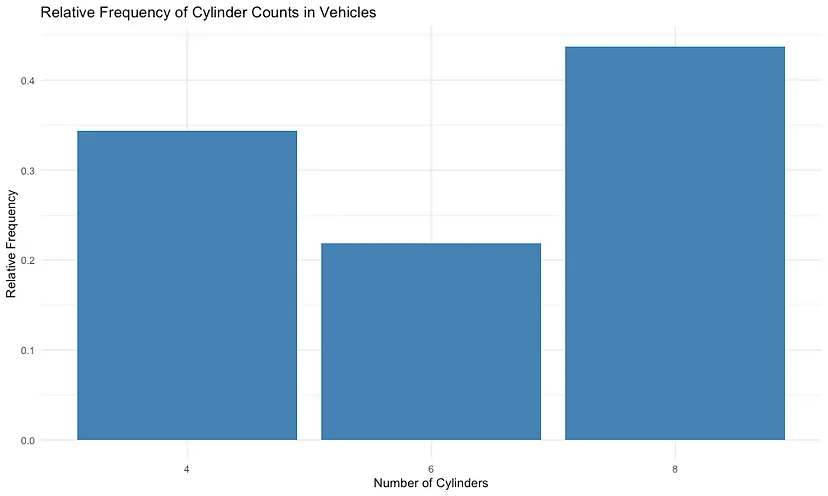

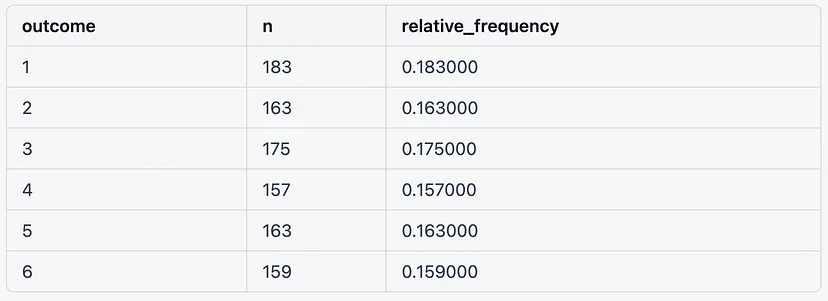
Another way to demonstrate the relative frequency approach is to simulate a die experiment, we will roll a fair six-sided die 1000 times and calculate the relative frequency of each outcome (1, 2, 3, 4, 5, and 6). Additionally, we will visualize the results using ggplot2.

set.seed(42) # Set seed for reproducibility
n_rolls <- 1000
die_rolls <- sample(1:6, size = n_rolls, replace = TRUE)

die_rolls_df <- data.frame(outcome = die_rolls) %>%
  count(outcome) %>%
  mutate(relative_frequency = n / n_rolls)

die_rolls_df

This will generate a data frame with the outcome, count, and relative frequency of each die roll:

Now, let’s create a bar chart to visualize the relative frequencies:

ggplot(die_rolls_df, aes(x = factor(outcome), y = relative_frequency)) +
  geom_col(fill = "steelblue") +
  labs(title = "Die Roll Simulation",
       x = "Outcome",
       y = "Relative Frequency") +
  theme_minimal()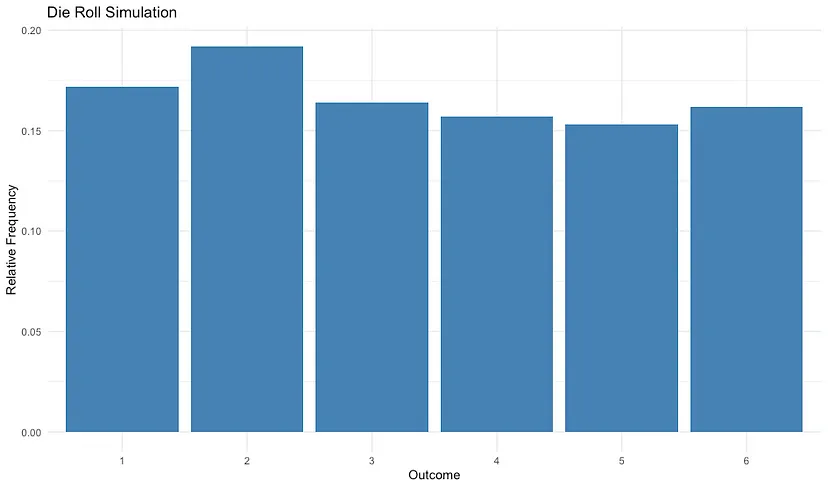

The resulting bar chart displays the relative frequencies of each outcome from the die roll simulation. The chart illustrates the concept of relative frequency by showing the proportion of each outcome observed in the experiment.

III. Probability Rules:

Addition Rule: The addition rule helps us calculate the probability of either event A or event B (or both) occurring. The rule is defined as:

P(A ∪ B) = P(A) + P(B) — P(A ∩ B)

Here, P(A ∪ B) represents the probability of event A or event B occurring, while P(A ∩ B) denotes the probability of both events A and B happening together.

Example: Suppose we have a deck of 52 playing cards. What is the probability of drawing either a red card (hearts or diamonds) or a queen?

There are 26 red cards and 4 queens in the deck, but 2 of the queens are also red cards (queen of hearts and queen of diamonds). So, applying the addition rule:

P(Red ∪ Queen) = P(Red) + P(Queen) — P(Red ∩ Queen)
P(Red ∪ Queen) = (26/52) + (4/52) — (2/52) = 28/52 ≈ 0.5385

Multiplication Rule: The multiplication rule helps us determine the probability of both events A and B occurring simultaneously. The rule is defined as:

P(A ∩ B) = P(A|B) * P(B)

Here, P(A|B) represents the probability of event A occurring given that event B has occurred.

Example: Consider a bag containing 5 blue and 3 red balls. We draw two balls from the bag without replacement. What is the probability of drawing a blue ball first, followed by a red ball?

To apply the multiplication rule, we first calculate the probability of each event:

P(Blue1) = 5/8 P(Red2|Blue1) = 3/7

Now, we can compute the probability of both events happening together:

P(Blue1 ∩ Red2) = P(Blue1) * P(Red2|Blue1) = (5/8) * (3/7) ≈ 0.2679

In the next part of this series, we will cover topics related to Descriptive Statistics.

For more practical tips and insights on AI, data science, and statistics, explore our blog at Analytica Data Science Solutions. Discover engaging content to expand your knowledge and stay up-to-date with the latest developments.

In this blog post, we have covered the basics of probability and statistics. If you wish to further expand your knowledge and understanding, here are some references to help you dive deeper into these topics:

Books:

1. DeGroot, M. H., & Schervish, M. J. (2012). Probability and Statistics (4th ed.). Pearson.
2. Wackerly, D., Mendenhall, W., & Scheaffer, R. L. (2007). Mathematical Statistics with Applications (7th ed.). Cengage Learning.
3. Casella, G., & Berger, R. L. (2001). Statistical Inference (2nd ed.). Duxbury Press.
4. Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer.
5. Wickham, H., & Grolemund, G. (2016). R for Data Science: Import, Tidy, Transform, Visualize, and Model Data. O’Reilly Media.

Websites:

1. Khan Academy — Probability and Statistics: https://www.khanacademy.org/math/statistics-probability
2. Stat Trek — Teach yourself statistics: https://stattrek.com/
3. Carnegie Mellon University Probability & Statistics: https://oli.cmu.edu/courses/probability-statistics-open-free/

Online Courses:

1. Coursera — Statistics with R Specialization by Duke University: https://www.coursera.org/specializations/statistics
2. Coursera — Introduction to Probability and Data with R by Duke University: https://www.coursera.org/learn/probability-intro
3. edX — Probability and Statistics in Data Science using Python by the University of California, San Diego: https://www.edx.org/course/probability-and-statistics-in-data-science-using-python
4. DataCamp — Introduction to Probability in R: https://www.datacamp.com/courses/introduction-to-probability-in-r
5. DataCamp — Foundations of Probability in R: https://www.datacamp.com/courses/foundations-of-probability-in-r

Read More blogs in AnalyticaDSS Blogs here : BLOGS

Read More blogs in Medium : Medium Blogs