“Riemann Hypothesis”

Welcome to the realm of unsolved mathematical riddles, where the limits of human comprehension are stretched to the furthest and the seemingly impossible becomes feasible. The Riemann Hypothesis, one of mathematics’s most perplexing and fascinating unresolved puzzles, will be the focus of today’s discussion.

For more than 150 years

For more than 150 years, the finest mathematicians have been enthralled by this conjecture, which was put out by the famous mathematician Bernhard Riemann in 1859. It asserts that the real component of any non-trivial Riemann zeta function zero is equal to 1/2 and that this property is connected to the distribution of prime numbers. Many have attempted and failed to solve this conundrum, which has not yet been fully understood. Whoever can either confirm or refute this idea will win a million dollars. It is a conundrum that has the potential to alter how we perceive both the world and mathematics. Are you prepared to start this exploration journey? Let’s reveal the Riemann Hypothesis’s mysteries and learn the secrets it conceals.

“Join us on a journey to explore the realm of unsolved mathematical riddles, where we will stretch the limits of human comprehension and make the seemingly impossible possible. Today, we will focus on the Riemann Hypothesis, one of mathematics’ most perplexing and fascinating unsolved puzzles. For more than 150 years, mathematicians have been captivated by this conjecture proposed by Bernhard Riemann in 1859. It states that the real component of any non-trivial Riemann zeta function zero is equal to 1/2 and that this property is connected to the distribution of prime numbers. Many have tried and failed to solve this conundrum, which remains a mystery. Solve it and win a million dollars. Are you ready to uncover the mysteries of the Riemann Hypothesis and learn its secrets?”

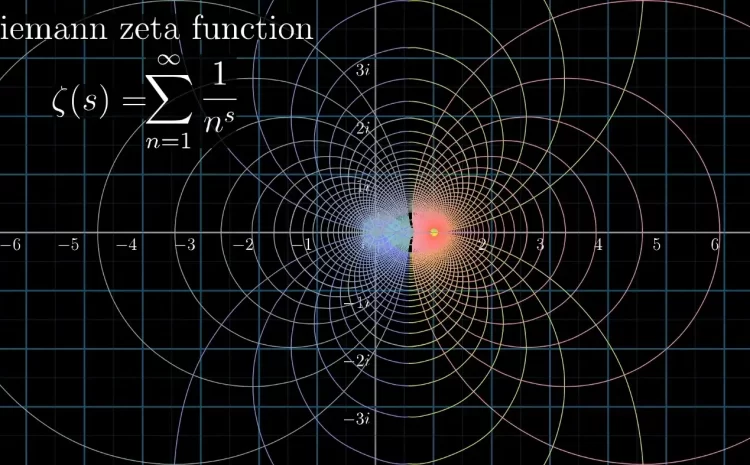
The Riemann zeta function is defined as:

ζ(s) = 1^(−s) + 2^(−s) + 3^(−s) + 4^(−s) + …

where in this case, s is a complex number, made of real an imaginary parts. Zeros of the Riemann zeta function that do not lie on the line (1/2 + it), where t is a real integer and i is the imaginary unit, are considered to be non-trivial zeros.

The Riemann Hypothesis

The Riemann Hypothesis is a significant unsolved issue in number theory with ramifications in a wide range of mathematical, physical, and cryptographic fields. For instance, proving the Riemann Hypothesis will help us better understand the prime number distribution since prime number distribution and Riemann zeta function zeros are closely connected.

Despite the huge effort of some of the brightest minds in history, proof or counterexample of the Riemann Hypothesis has yet to be found. However, many important results have been obtained and progress has been made toward a proof. For example, the first million zeros of the Riemann zeta function were computed and all lie in the critical strip, which is the region where the Riemann Hypothesis states they should be.

Examining how the Riemann Hypothesis relates to other significant mathematical puzzles will help you comprehend it better. For instance, the Goldbach Conjecture asserts that the sum of any two prime integers may be used to represent any even integer bigger than 2. According to the Twin Prime Conjecture, there exist an unlimited amount of prime numbers that differ by 2. These two issues have been demonstrated to be tied to the Riemann Hypothesis and are intimately related to the prime number distribution.

In terms of progress towards a proof

In terms of progress towards a proof, many important results have been obtained. For example, the first million zeros of the Riemann zeta function have been computed and all lie on the critical line, as predicted by the Riemann Hypothesis. Additionally, many other important results have been obtained that provide evidence for the truth of the Riemann Hypothesis. However, a proof or counterexample has yet to be found.

Mathematics and many other disciplines would be greatly impacted by a demonstration of the Riemann Hypothesis. The distribution of primes would be better understood as a result, and it would also open up new avenues for thinking about other significant mathematical issues. Physics and other fields, including encryption, would also be affected.

Riemann zeta

By identifying the Riemann zeta function’s non-trivial zeros that fall on the crucial line 1/2 + it, one may use code examples to demonstrate how to computationally verify the Riemann Hypothesis. To get the first few zeta zeros in Python and R, respectively, utilize the code samples I gave previously.

In conclusion, the Riemann Hypothesis is a stunning and complex subject that has captivated mathematicians for more than 150 years and offers a $1 million prize for a proof or counterexample. It has ramifications for many branches of mathematics, as well as physics and cryptography, and is connected to the distribution of prime numbers. Although it’s still up for debate, significant findings have been discovered, and work toward a proof has advanced.

Read More blogs in AnalyticaDSS Blogs here : BLOGS

Read More blogs in Medium : Medium Blogs